最近学习了吴恩达的machine learning前5周的课程，收获很大，不过发现以前的知识不用很快就会忘记，所以纪录一下，以便以后快速查阅。

what is machine learning?

比较典型简单的machine learning应用例如邮件分别是不是诈骗垃圾邮件，

Machine learning 这个词语并不新鲜，早在1959年，Arthur Samuel提出machine learning的定义：

Field of study that gives computers the ability to learn without being explicitly programmed.

Tom Mitchell在1998年提出well-posed learning problem(自适应学习问题)：> A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

机器学习算法可以分为：

1. supervised learning（有监督的学习）
2. unsupervised learning(无监督学习)
3. reinforcement learning(增强学习)
4. recommender systems（推荐系统）

在这个课程中着重讲前两种算法。

supervised learning

什么是有监督学习？就是在学习的时候有正确答案在“监督”着training的过程。

有监督学习有这样几种经典应用：

归化问题（线性或非线性)

预测房子房价,根据现有的房子面积和房价数据，来预测更大面积的房子价格

图1

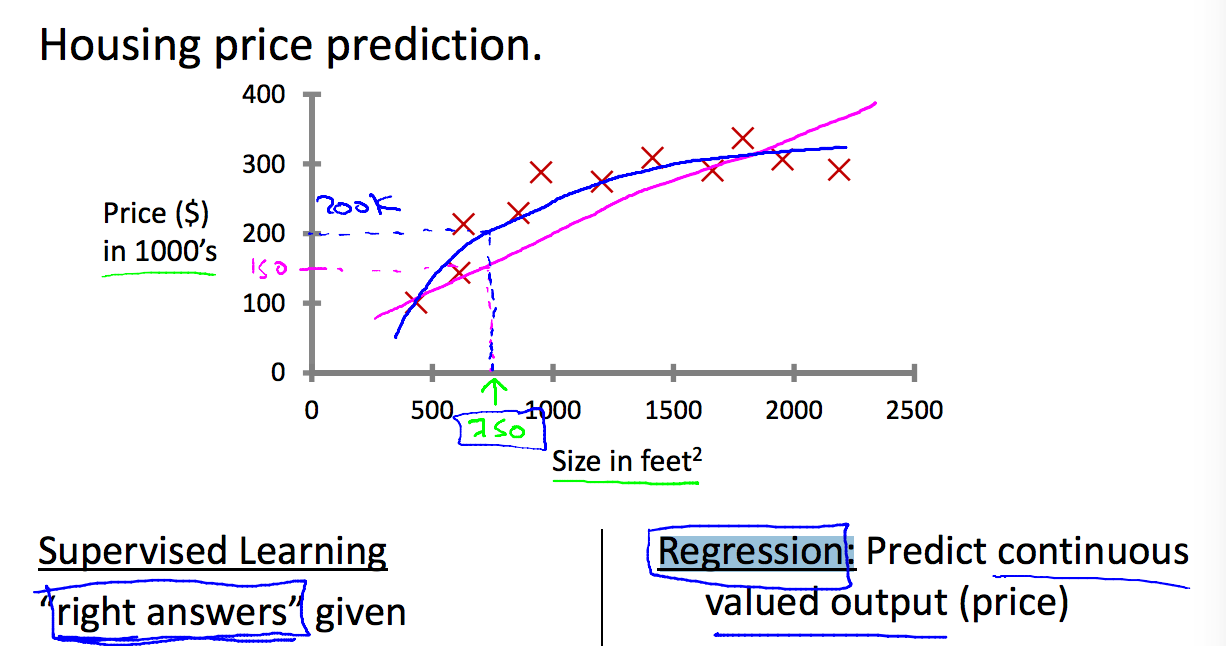
分类问题

乳腺癌的肿瘤是否是恶性肿瘤问题。根据肿瘤的大小和是否是恶性肿瘤分类：

图2

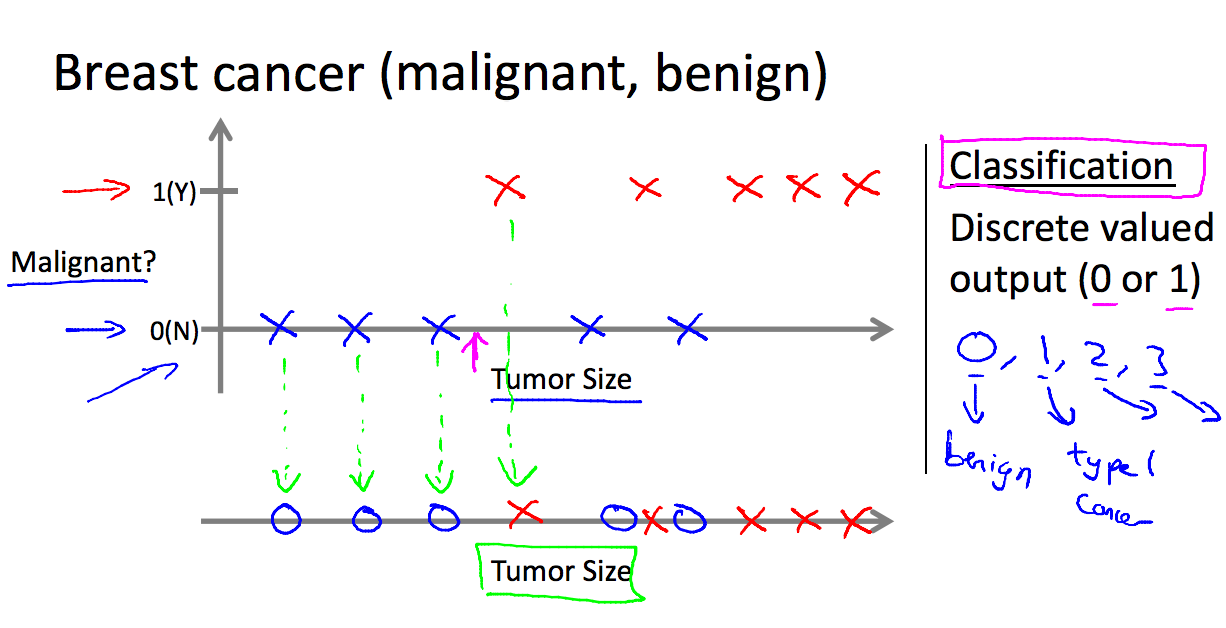
unsupervised learning

无监督学习与有监督学习的不同就是在training的时候并不知道样本的属性和标签，没人告诉我们应该怎么做，没人告诉我们每个样本代表着什么。如果给定一个数据集，无监督学习可能判断结果包含两种聚类，就是所谓的聚类算法。

图3

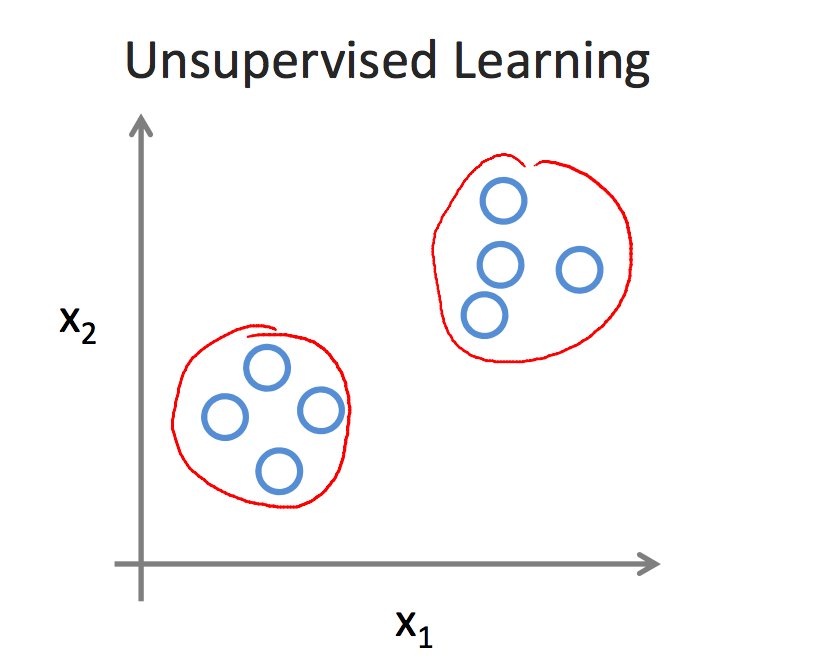
聚类算法有广泛的应用，例如大数据中心的集群管理，社交人群的分类分析等。

图4

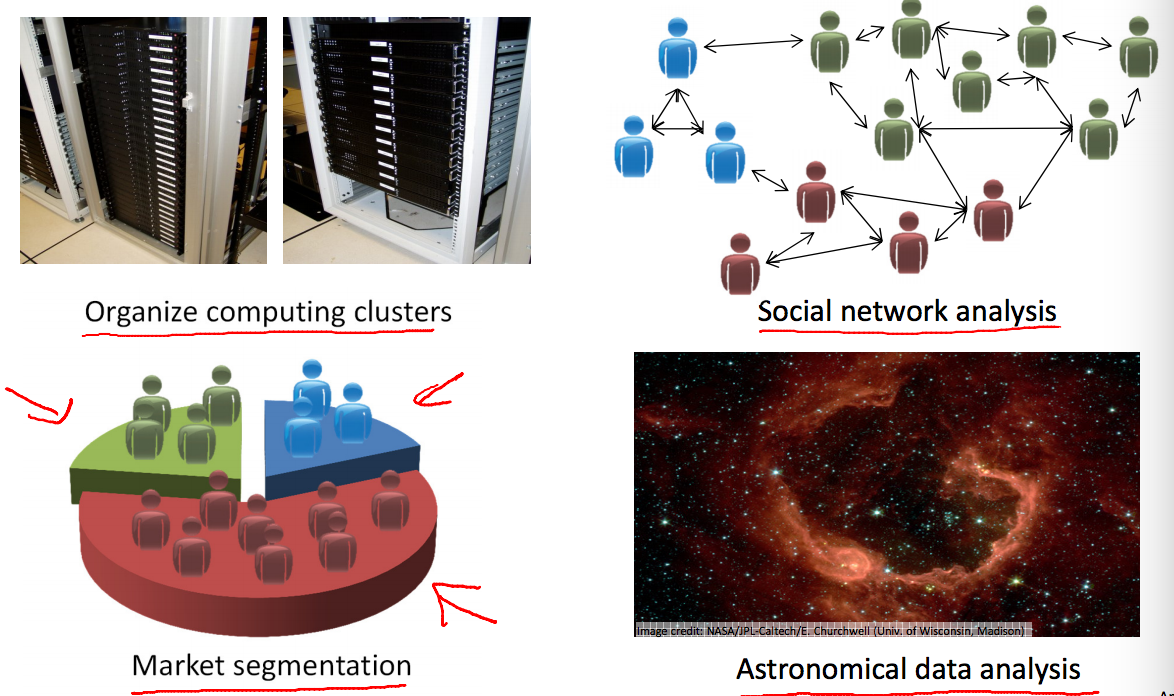
简单介绍完机器学习的类型，下面开始看监督学习中归化问题如何进行建模

model representation

假设给定了一组在portland的房价信息，我们用m来标记training的样本数，x用来表示输入的变量和特征，y用来表示输出：

图5

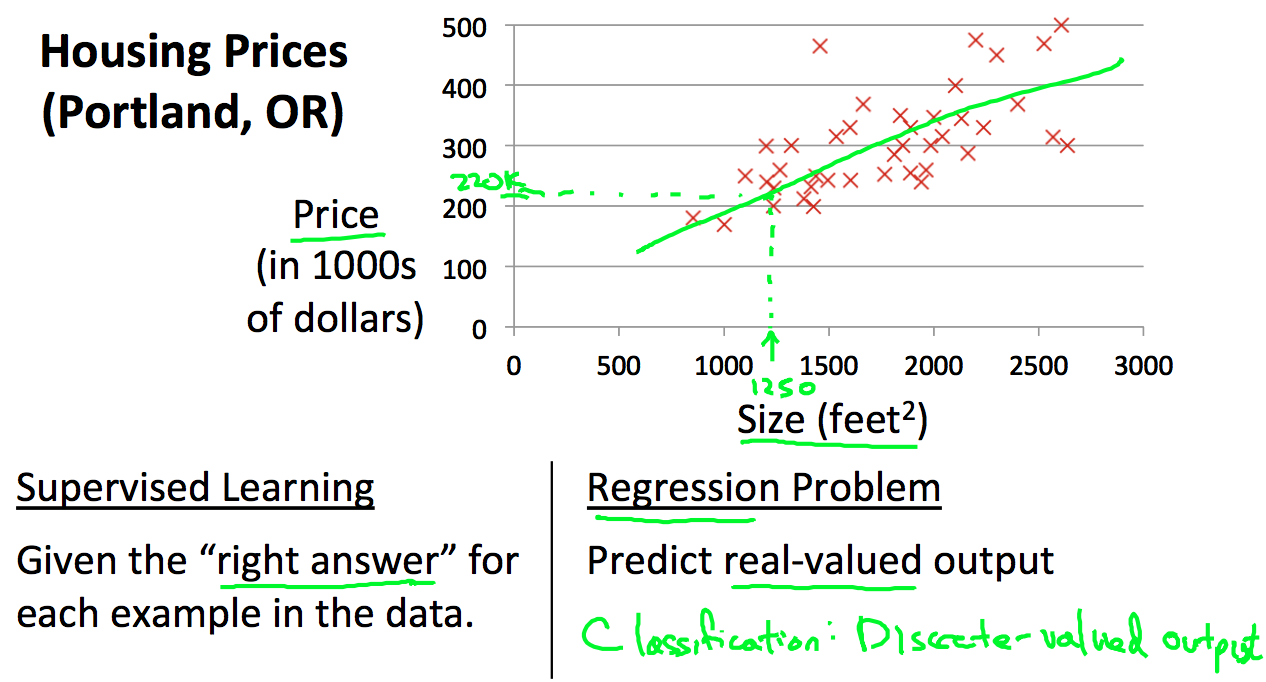
我们可以看到，学习算法需要训练数据的学习，然后给出一个预测（hypothesis，简称h），那么我们怎么表示h？

图6

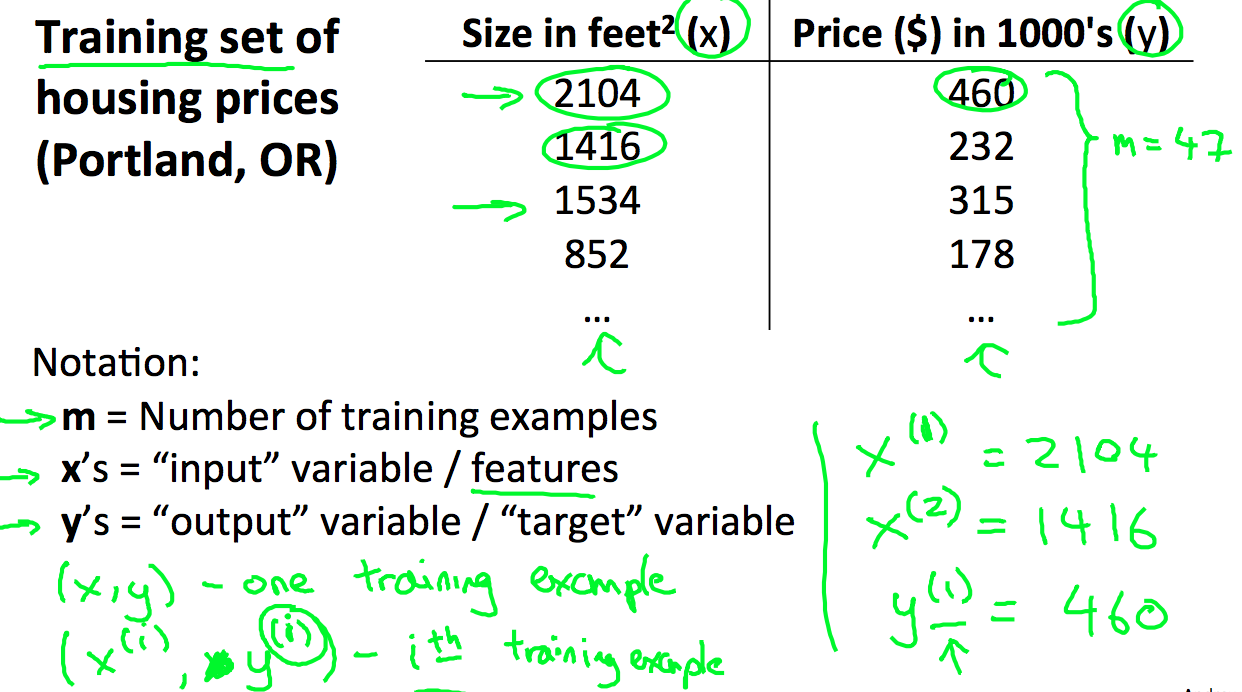
一个变量的线性归化

因为只有一个变量，那么我们可以这样表示h：

图7

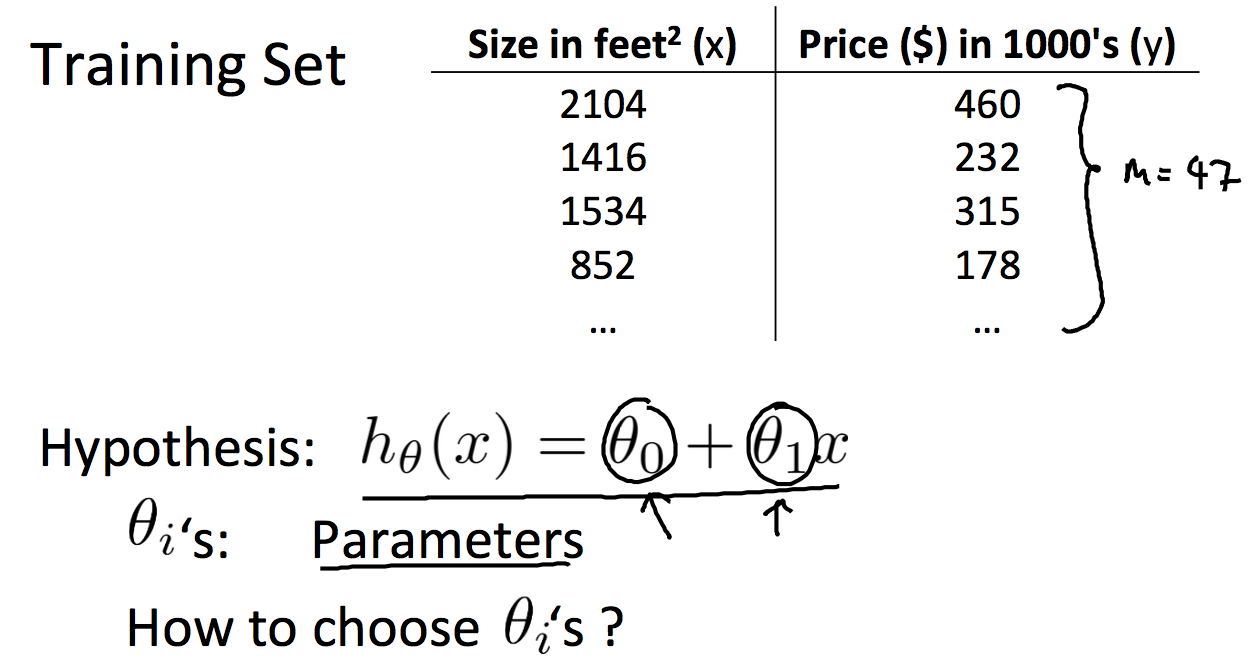
那么该怎么选择两个theta参数？这边就引出cost function的概念。

cost function

cost function就是表征你的预测h和实际的值之间的差别。所以我们的目标是cost function越小越好，直到找到最小值。我们用J表示cost function的值。

图8

举个例子，我们要对图中三个红叉数据进行归化，那么我们先取theta1为0.5，那么cost function的结果是0.58，接着取theta为0，结果是2.3， 取theta1为1，结果是0，就这样一步一步的选取不同的theta值，计算cost function，画出如右图的图标，可以看到theta为1的时候，得到J的最小值。

图9

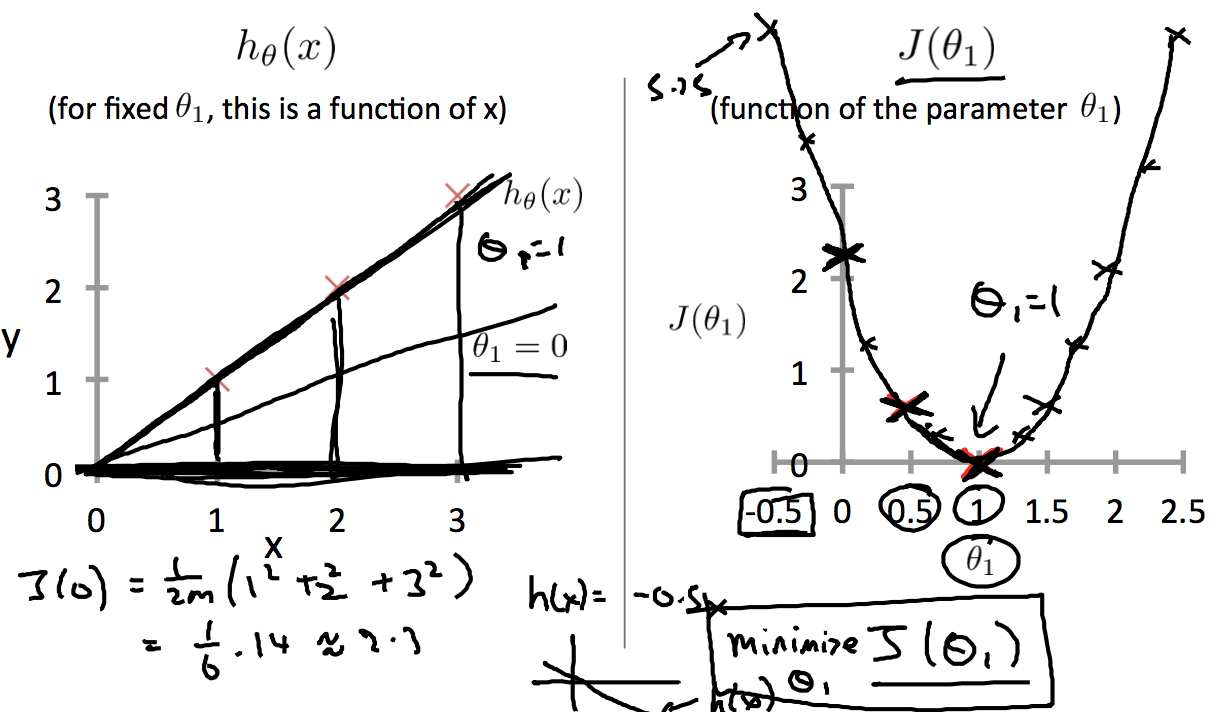
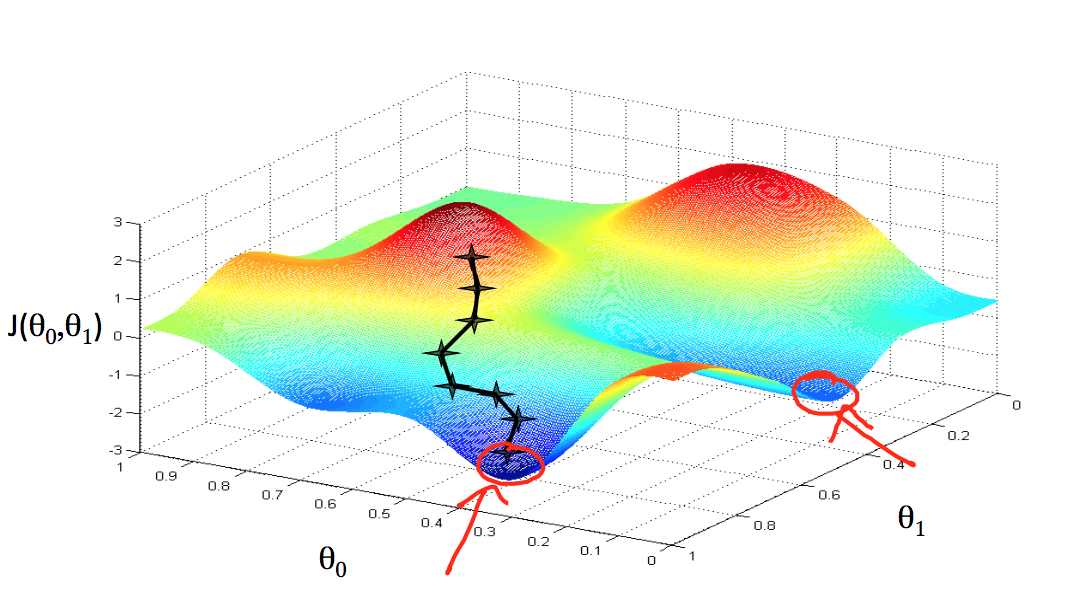
这是只变化一个theta值的J的变化，两个theta值一起变化就得到一个三维图，如下图所示，是一个碗装的形状。

图10

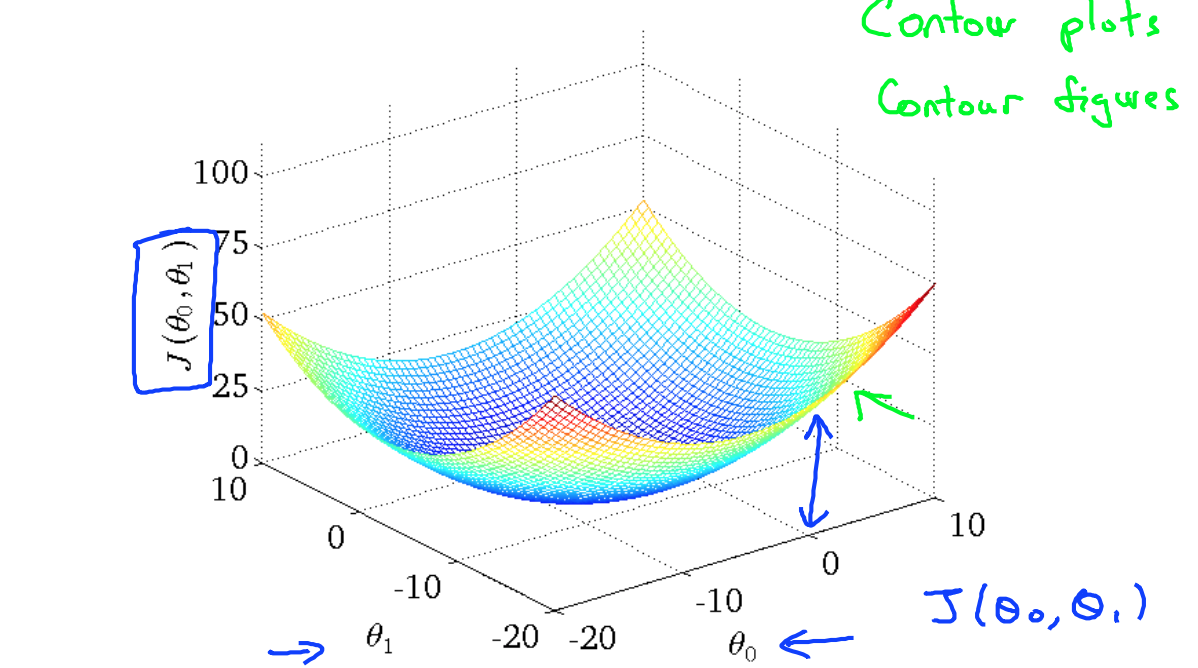
gradient descent（梯度下降）

我们有一个cost function J， 想要它的最小值，我们要如何寻找到最适合的参数？这就需要用到梯度下降算法：

1. 从某个theta1，theta2初始值开始
2. 不断改变theta1，theta2来不断减小

这个算法的关键点就是下一个theta值应该如何变化？梯度下降法就给出了这样的算法：

图11

我们可以看到，变化是减去一个学习率和cost function J的偏导数相乘的结果。当偏导数为正的时候，说明J的斜率是如下图上图所示，所以theta减去一个正数会变小，所以theta应该向左移动，反之亦然，最终帮助我们找到J的最小值。

图12

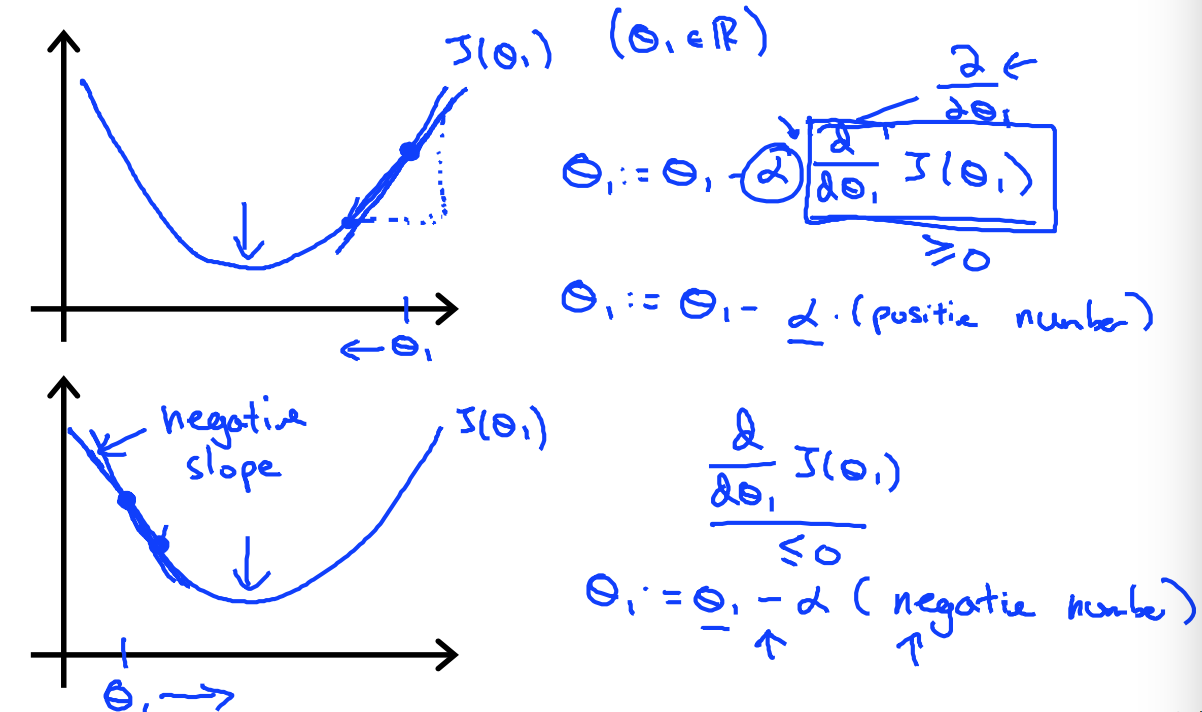
那么学习率在这里是什么作用呢？起到决定每次theta变化的大小，如果学习率很小，会导致每次theta变化很小，整个梯度下降过程会计算很多步，很慢才能找到结果，如果太大的话，有何能会错过极小值。

图13

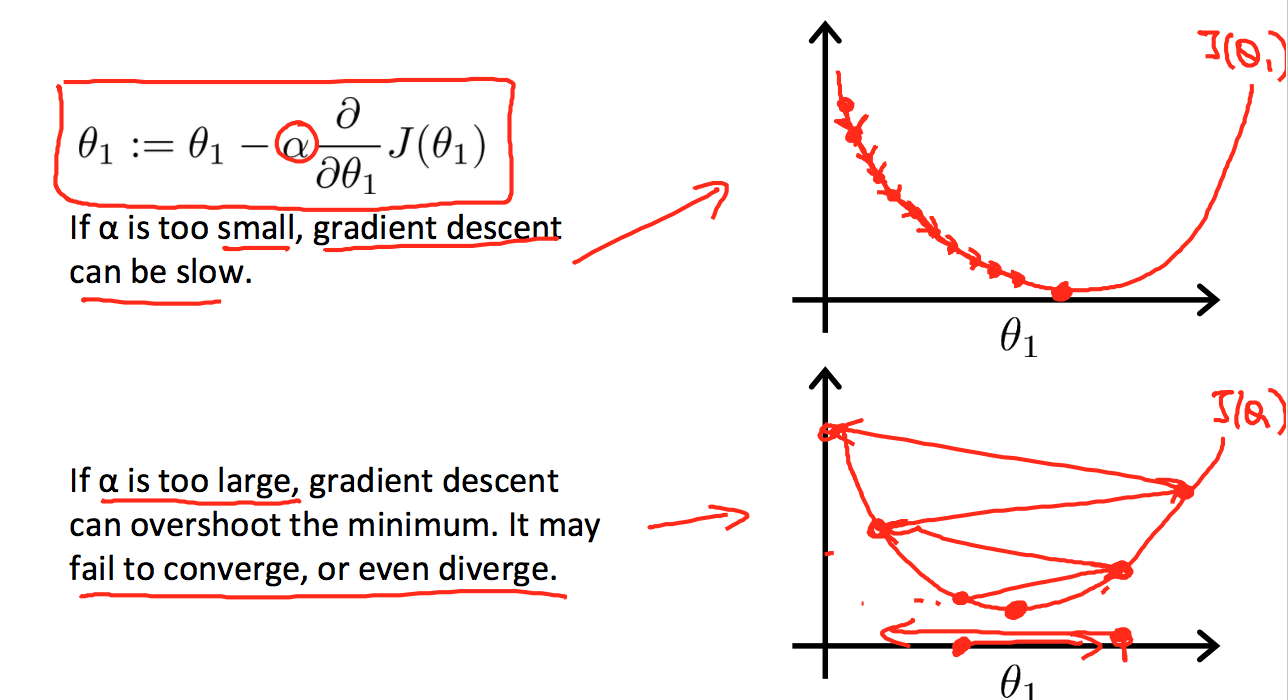
线性归化的梯度下降

根据上面梯度下降的的公式结合线性回归的cost function公式：

图14

把J带入到梯度下降公式中：

图15

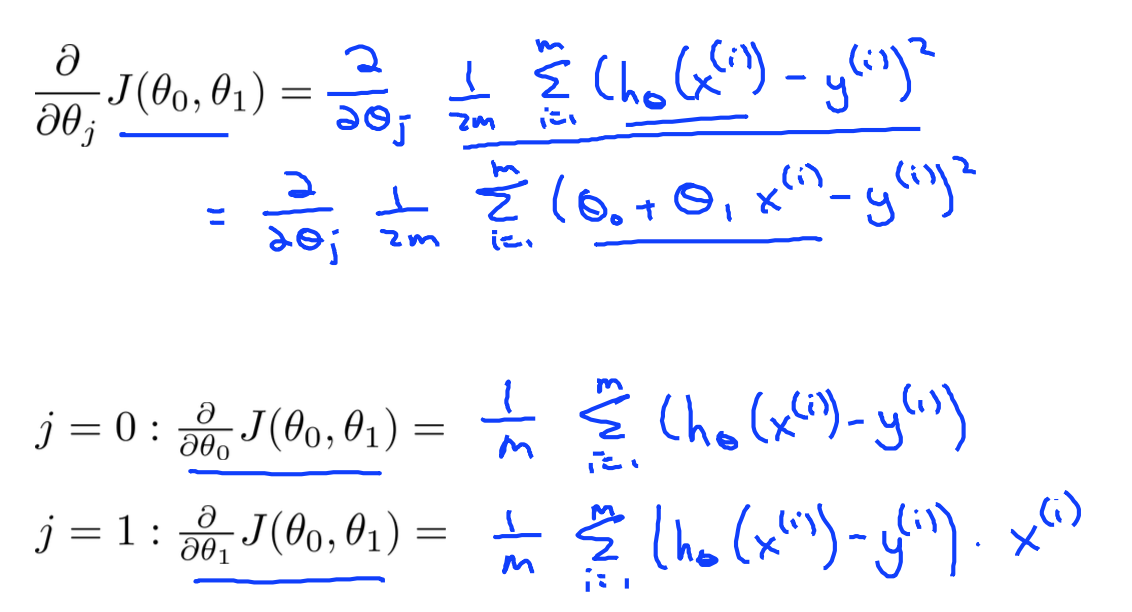
那么可得：

图16

梯度下降算法就会带领一条路径，帮助你快速找到那个最低点：

图17